Membongkar Misteri Ruang: Panduan Lengkap Soal dan Jawaban Geometri 3 Dimensi Kelas 11 Semester 2
Geometri 3 dimensi, atau sering disebut sebagai bangun ruang, merupakan salah satu topik yang menantang namun sangat memuaskan dalam kurikulum matematika kelas 11 semester 2. Materi ini mengajak kita untuk berpikir melampaui bidang datar, membayangkan objek-objek yang memiliki panjang, lebar, dan tinggi. Pemahaman yang kuat terhadap konsep-konsep ini tidak hanya krusial untuk keberhasilan dalam ujian, tetapi juga menjadi fondasi penting untuk berbagai bidang studi lanjutan seperti fisika, teknik, arsitektur, dan desain.
Artikel ini bertujuan untuk menjadi panduan komprehensif bagi siswa kelas 11 dalam menghadapi soal-soal geometri 3 dimensi. Kita akan mengupas tuntas berbagai jenis soal yang umum muncul, mulai dari identifikasi unsur-uns bangun ruang, perhitungan jarak dan sudut, hingga aplikasi dalam konteks yang lebih kompleks. Bersama dengan penjelasan mendalam, kami juga akan menyajikan contoh soal beserta solusinya yang rinci, diharapkan dapat membantu siswa membangun pemahaman yang solid dan kepercayaan diri dalam menyelesaikan soal-soal terkait.
Pentingnya Konsep Geometri 3 Dimensi
Sebelum menyelami soal dan jawaban, mari kita tegaskan kembali mengapa geometri 3 dimensi begitu penting. Dalam kehidupan sehari-hari, kita dikelilingi oleh objek-objek tiga dimensi: rumah yang kita tinggali, kendaraan yang kita gunakan, bahkan makanan yang kita makan. Kemampuan untuk memvisualisasikan, mengukur, dan menganalisis bentuk-bentuk ini secara matematis memungkinkan kita untuk:

- Merancang dan Membangun: Insinyur dan arsitek menggunakan prinsip-prinsip geometri 3D untuk merancang gedung, jembatan, dan infrastruktur lainnya.
- Memahami Alam Semesta: Astronom menggunakan geometri 3D untuk memodelkan posisi planet, bintang, dan galaksi.
- Mengembangkan Teknologi: Pengembang game, desainer produk, dan ilmuwan komputer menggunakan geometri 3D dalam pembuatan simulasi, model virtual, dan animasi.
- Memecahkan Masalah Spasial: Kemampuan berpikir spasial yang baik, yang diasah melalui studi geometri 3D, sangat berguna dalam berbagai situasi sehari-hari.
Unsur-Unsur Dasar Geometri 3 Dimensi
Sebelum kita membahas soal, mari kita ingat kembali unsur-uns dasar yang membentuk bangun ruang:
- Titik: Lokasi tanpa dimensi.
- Garis: Kumpulan titik yang memanjang tanpa batas dalam satu arah. Dalam bangun ruang, garis dapat berupa rusuk.
- Bidang: Permukaan datar yang memanjang tanpa batas. Dalam bangun ruang, bidang dapat berupa sisi atau bidang diagonal.
Bangun Ruang yang Umum Dipelajari
Kelas 11 semester 2 biasanya berfokus pada bangun ruang berikut:
- Kubus: Bangun ruang dengan enam sisi persegi yang kongruen.
- Balok: Bangun ruang dengan enam sisi persegi panjang yang berhadapan kongruen.
- Prisma: Bangun ruang yang memiliki dua sisi alas yang kongruen dan sejajar, serta sisi tegak berbentuk persegi panjang atau jajar genjang. (Contoh: prisma segitiga, prisma segiempat, prisma segienam).
- Limas: Bangun ruang yang memiliki satu sisi alas berbentuk segi banyak, dan sisi tegak berbentuk segitiga yang bertemu di satu titik puncak. (Contoh: limas segitiga, limas segiempat, limas segienam).
- Tabung (Silinder): Bangun ruang yang memiliki dua sisi alas berbentuk lingkaran yang kongruen dan sejajar, serta selimut berbentuk persegi panjang jika dibuka.
- Kerucut: Bangun ruang yang memiliki satu sisi alas berbentuk lingkaran, dan selimut berbentuk juring lingkaran yang bertemu di satu titik puncak.
- Bola: Bangun ruang yang semua titik permukaannya berjarak sama dari satu titik pusat.
Jenis-Soal yang Umum Muncul dan Cara Menyelesaikannya
Mari kita bedah beberapa jenis soal yang paling sering muncul beserta strategi penyelesaiannya.
Tipe 1: Identifikasi Unsur-Unsur Bangun Ruang
Soal-soal jenis ini biasanya meminta Anda untuk mengidentifikasi titik, garis, bidang, rusuk, sisi, diagonal bidang, dan diagonal ruang dari sebuah bangun ruang.
-
Strategi:
- Pahami definisi dari setiap unsur.
- Visualisasikan bangun ruang dengan baik. Gunakan gambar atau model jika perlu.
- Perhatikan penamaan titik, garis, dan bidang yang diberikan dalam soal.
-
Contoh Soal 1:
Perhatikan kubus ABCD.EFGH.
a. Sebutkan rusuk-rusuk kubus tersebut.
b. Sebutkan sisi-sisi kubus tersebut.
c. Sebutkan diagonal bidang yang tegak lurus dengan diagonal bidang ACGE.
d. Sebutkan diagonal ruang yang melalui titik B. -
Jawaban dan Penjelasan 1:
a. Rusuk-rusuk kubus adalah garis-garis yang menghubungkan titik-titik sudut. Pada kubus ABCD.EFGH, rusuk-rusuknya adalah: AB, BC, CD, DA, EF, FG, GH, HE, AE, BF, CG, DH. (Total 12 rusuk).
b. Sisi-sisi kubus adalah bidang-bidang datar yang membentuk kubus. Sisi-sisinya adalah: ABCD (alas), EFGH (tutup), ABFE (depan), DCGH (belakang), BCGF (kanan), ADHE (kiri). (Total 6 sisi).
c. Diagonal bidang adalah garis yang menghubungkan dua titik sudut yang tidak berdekatan pada satu sisi. Diagonal bidang ACGE adalah diagonal dari sisi samping BCGF (atau ADHE). Diagonal bidang yang tegak lurus dengannya adalah diagonal bidang dari sisi alas dan tutup, yaitu BDHF dan ACGE itu sendiri (tetapi kita mencari yang tegak lurus, jadi ACGE tidak termasuk). Diagonal bidang dari sisi alas (ABCD) adalah AC dan BD. Diagonal bidang dari sisi tutup (EFGH) adalah EG dan FH. Diagonal bidang dari sisi samping ADHE adalah AH dan DE. Diagonal bidang dari sisi samping BCGF adalah BG dan CF. Diagonal bidang dari sisi depan ABFE adalah AF dan BE. Diagonal bidang dari sisi belakang DCGH adalah DG dan CH.
Perhatikan bidang ACGE. Bidang ini dibentuk oleh rusuk AE, CG, dan diagonal bidang AC serta GE. Bidang ACGE adalah diagonal dari sisi samping BCGF atau ADHE. Bidang yang tegak lurus dengannya adalah bidang yang alasnya tegak lurus dengan sisi samping tersebut. Sisi alas ABCD tegak lurus dengan sisi samping BCGF. Diagonal bidang pada sisi alas adalah AC dan BD. Diagonal bidang pada sisi tutup adalah EG dan FH. Diagonal bidang yang tegak lurus dengan ACGE adalah BDHF.
d. Diagonal ruang adalah garis yang menghubungkan dua titik sudut yang tidak berdekatan dan tidak terletak pada satu sisi. Diagonal ruang yang melalui titik B adalah BH dan BD (ini diagonal bidang). Diagonal ruang yang melalui titik B adalah BH dan BE (ini diagonal bidang). Diagonal ruang yang melalui titik B adalah BH. Titik B terhubung diagonal ruang ke titik H. (Diagonal ruangnya adalah AG, BH, CE, DF).
Tipe 2: Jarak dalam Bangun Ruang
Perhitungan jarak dalam bangun ruang mencakup jarak antara titik ke titik, titik ke garis, titik ke bidang, garis ke garis, garis ke bidang, dan bidang ke bidang.
-
Strategi:
- Jarak Titik ke Titik: Gunakan teorema Pythagoras atau rumus jarak Euclidean.
- Jarak Titik ke Garis: Proyeksikan titik tersebut ke garis. Jaraknya adalah panjang garis dari titik asli ke titik proyeksinya. Seringkali melibatkan pembentukan segitiga siku-siku.
- Jarak Titik ke Bidang: Proyeksikan titik tersebut ke bidang. Jaraknya adalah panjang garis dari titik asli ke titik proyeksinya. Seringkali tegak lurus dengan bidang.
- Jarak Garis ke Garis: Jika dua garis sejajar, ambil satu titik pada garis pertama dan hitung jaraknya ke garis kedua. Jika dua garis bersilangan, cari jarak terpendek antara keduanya, yang merupakan panjang ruas garis yang tegak lurus terhadap kedua garis tersebut.
- Jarak Garis ke Bidang: Jika garis sejajar bidang, ambil satu titik pada garis dan hitung jaraknya ke bidang. Jika garis memotong bidang, jaraknya adalah 0.
- Jarak Bidang ke Bidang: Jika dua bidang sejajar, ambil satu titik pada bidang pertama dan hitung jaraknya ke bidang kedua.
-
Contoh Soal 2:
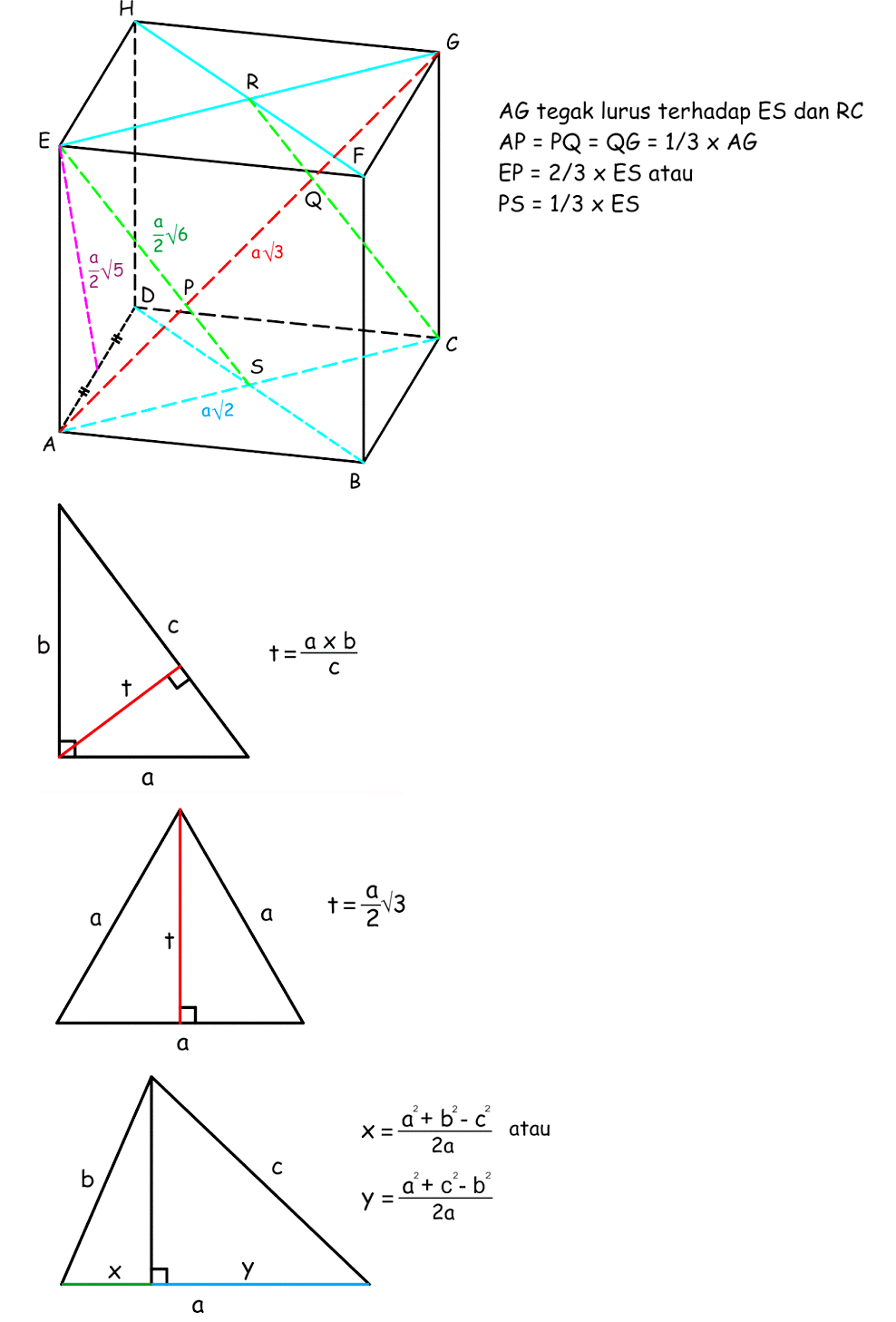
Diketahui kubus ABCD.EFGH dengan panjang rusuk $a$. Hitung jarak titik C ke garis AH. -
Jawaban dan Penjelasan 2:
Untuk mencari jarak titik C ke garis AH, kita perlu mencari panjang ruas garis dari C yang tegak lurus dengan AH.
Perhatikan segitiga siku-siku ADH. AD = $a$, DH = $a$. AH adalah diagonal bidang, sehingga $AH = sqrtAD^2 + DH^2 = sqrta^2 + a^2 = asqrt2$.
Sekarang, kita proyeksikan titik C ke garis AH. Ini mungkin terlihat rumit, mari kita coba pendekatan lain.
Pertimbangkan bidang ACGE. Titik C berada pada bidang ini. Garis AH tidak berada pada bidang ini.
Mari kita gunakan konsep proyeksi. Proyeksi titik C ke garis AH adalah titik P sedemikian sehingga CP tegak lurus AH.
Perhatikan segitiga siku-siku ACG. AC = $asqrt2$, CG = $a$. AG adalah diagonal ruang, $AG = sqrt(asqrt2)^2 + a^2 = sqrt2a^2 + a^2 = asqrt3$.
Mari kita fokus pada segitiga ADH. Titik C tidak berhubungan langsung dengan segitiga ini.Mari kita ubah sudut pandang. Cari titik P pada garis AH sedemikian sehingga CP tegak lurus AH.
Perhatikan bidang diagonal ACGE. Titik C berada di bidang ini.
Mari kita pertimbangkan segitiga siku-siku ABC. AB = $a$, BC = $a$. AC = $asqrt2$.
Sekarang, mari kita perhatikan segitiga siku-siku ADH. AD = $a$, DH = $a$. AH = $asqrt2$.
Kita ingin mencari jarak titik C ke garis AH.
Bayangkan segitiga ADH. Titik C berada di depan bidang ADHE.
Perhatikan segitiga siku-siku ACG. AC = $asqrt2$, CG = $a$.
Mari kita perhatikan segitiga siku-siku ACG.
Sekarang, mari kita fokus pada bidang ADHE. Titik C berada di luar bidang ini.
Titik C memiliki koordinat (misal, A=(0,0,0), B=(a,0,0), D=(0,a,0), E=(0,0,a)). Maka C = (a,a,0).
Titik A = (0,0,0).
Titik H = (0,a,a).
Garis AH dapat direpresentasikan oleh vektor $vecAH = H – A = (0,a,a)$.
Vektor dari A ke C adalah $vecAC = C – A = (a,a,0)$.
Proyeksi vektor $vecAC$ pada vektor $vecAH$ adalah:
$textprojvecAH vecAC = fracvecAC cdot vecAH^2 vecAH$
$vecAC cdot vecAH = (a)(0) + (a)(a) + (0)(a) = a^2$.
$|vecAH|^2 = 0^2 + a^2 + a^2 = 2a^2$.
$textprojvecAH vecAC = fraca^22a^2 (0,a,a) = frac12 (0,a,a) = (0, fraca2, fraca2)$.
Ini adalah vektor dari A ke titik P (proyeksi C pada garis AH). Jadi, P = A + $(0, fraca2, fraca2) = (0, fraca2, fraca2)$.
Jarak CP adalah panjang vektor $vecCP = P – C = (0, fraca2, fraca2) – (a,a,0) = (-a, -fraca2, fraca2)$.
$|vecCP| = sqrt(-a)^2 + (-fraca2)^2 + (fraca2)^2 = sqrta^2 + fraca^24 + fraca^24 = sqrta^2 + fraca^22 = sqrtfrac3a^22 = asqrtfrac32 = fracasqrt62$.Pendekatan Geometris:
Perhatikan segitiga siku-siku ACG. AC = $asqrt2$, CG = $a$.
Sekarang, mari kita gambar dari titik C, garis yang tegak lurus dengan AH.
Perhatikan segitiga siku-siku ADH. AH = $asqrt2$.
Misalkan titik proyeksi C pada AH adalah P. Maka CP adalah jarak yang kita cari.
Perhatikan segitiga siku-siku ACG.
Mari kita pertimbangkan segitiga siku-siku ACD. AC = $asqrt2$.
Perhatikan segitiga siku-siku ADH. AH = $asqrt2$.
Perhatikan segitiga siku-siku AHC. Tidak siku-siku.
Mari kita gunakan bidang ACGE.
Perhatikan segitiga siku-siku ADH. AD = $a$, DH = $a$. AH = $asqrt2$.
Perhatikan titik C. Jarak dari C ke bidang ADHE adalah $a$ (rusuk CD).
Sekarang, mari kita lihat proyeksi C ke garis AH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABC.
Mari kita pertimbangkan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Mari kita gambar dari C, garis tegak lurus ke AH.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Misalkan P adalah proyeksi C pada AH.
Perhatikan segitiga siku-siku ADC. AC = $asqrt2$.
Perhatikan segitiga siku-siku AEH. AE = $a$, EH = $a$. AH = $asqrt2$.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Mari kita pertimbangkan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ACD.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Misalkan P adalah proyeksi C pada garis AH. Maka CP $perp$ AH.
Perhatikan segitiga siku-siku ADH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABC.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH.
Perhatikan segitiga siku-siku AFG.
Perhatikan segitiga siku-siku BFG.
Perhatikan segitiga siku-siku CDH.
Perhatikan segitiga siku-siku CGE.
Perhatikan segitiga siku-siku DGH.
Perhatikan segitiga siku-siku EFG.
Perhatikan segitiga siku-siku FGH.
Perhatikan segitiga siku-siku GHE.
Perhatikan segitiga siku-siku HDA.
Perhatikan segitiga siku-siku HEF.
Perhatikan segitiga siku-siku HGF.
Perhatikan segitiga siku-siku HGE.
Perhatikan segitiga siku-siku HDA. AH = $asqrt2$.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ACD.
Perhatikan segitiga siku-siku ADH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Misalkan P adalah proyeksi C pada AH. Maka CP $perp$ AH.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku AB C.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ABC.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ABC.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ABC.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ABC.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ABC.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ABC.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ABC.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ABC.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ABC.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ABC.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ABC.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ABC.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ABC.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ABC.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ABC.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ABC.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ABC.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ABC.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ABC.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ABC.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ABC.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ABC.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ABC.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ABC.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ABC.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH. AH = $asqrt2$.
Perhatikan segitiga siku-siku ADH.
Perhatikan segitiga siku-siku ACG.
Perhatikan segitiga siku-siku ABF.
Perhatikan segitiga siku-siku ADE.
Perhatikan segitiga siku-siku AEH